Ask a Question

Which of the following statements is true only if triangles EFI and GFH are similar?

in Education by (257k points)

Question: Which of the following statements is true only if triangles EFI and GFH are similar?

getvoice-triangle

Options:

  1.  Two segment FI equals three segment FH
  2.  Segment FH over segment FI equals segment HG over segment IE
  3.  Points E, F, and G are collinear
  4.  ∠F ≅ ∠G

Please log in or register to answer this question.

1 Answer

+1 vote
by (735k points)
selected by
 
Best answer

2. Segment FH over segment FI equals segment HG over segment IE

If triangles EFI and GFH are similar then, the statement

triangle-smiliar

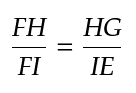
is correct.

Solution:

The triangles EFI and GFH are similar. So, their corresponding angles are congruent and the corresponding sides are in proportion.

So,

EF corresponds to GF
FI corresponds to FH
IE corresponds to HG

Using properties of similarity of triangle, we can say;

FI/FH = IE/HG

which is the same as

FH/FI = HG/IE

Basically, the corresponding sides create equal ratios to form this proportion.

So,

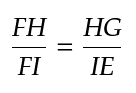
triangle-similarity

Hence, proved.

Related questions

...